EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software

Hosted by

Introduction to dual models

• a fine (high density) FEM, on which to perform the forward model (calculate measurements from parameters), and
• a coarse (lower density) FEM, on which to perform the inverse problem (reconstructing image parameters from measurements)

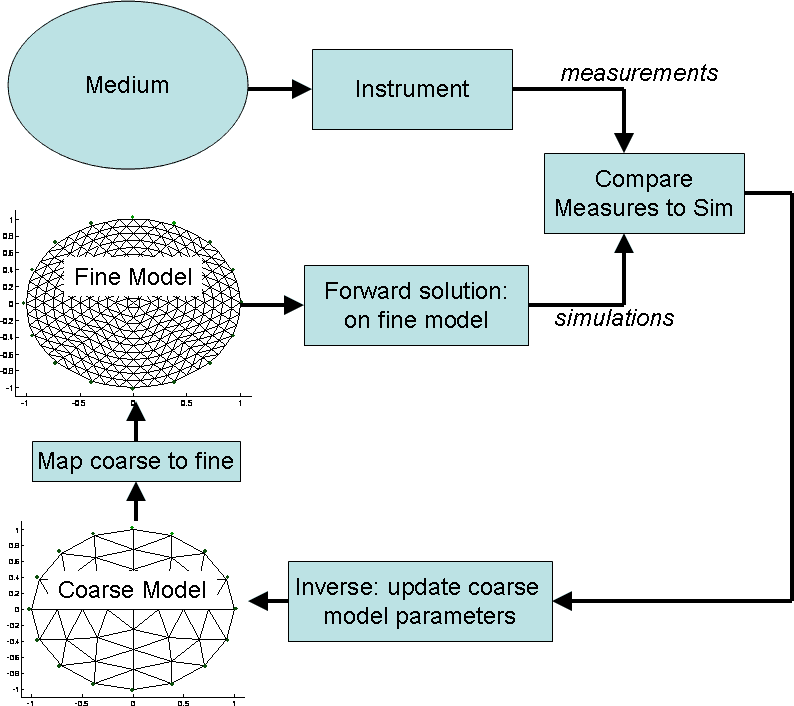
Figure: Schematic of a dual model based inverse problem

Simulated data

% Simulate data $Id: dual_model01.m 2162 2010-04-04 20:49:45Z aadler $
imdl= mk_common_model('c2c2',16);
img= mk_image(imdl);
vh=fwd_solve(img);
idx=[365,328,292,259,227,198,170,145,121];
img.elem_data([idx,idx+1,101,81])=1.1;
vi=fwd_solve(img);

show_fem(img);
print_convert('dual_model01a.png', '-density 60');

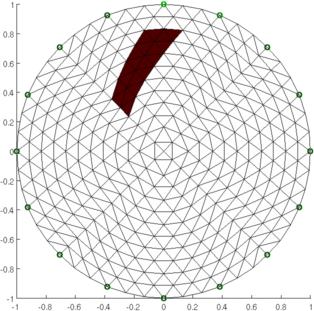
Figure: Simulation data

Simple Example: Dual model using multi-element parameters

1. A 64 element mesh where the fine==coarse mesh. There are 64 conductivity parameters to solve
2. A 64 element mesh where 4 inner elements have the same conductivity. Thus there are 64-(4-1)=61 conductivity parameters to solve
3. A 64 element mesh where 9 elements in an inner pie slice have the same conductivity. Thus there are 64-(9-1)=56 conductivity parameters to solve

% Simulate data $Id: dual_model02.m 4839 2015-03-30 07:44:50Z aadler $

% create base model
mdl_base=mk_common_model('a2c0',16);
mdl_base.RtR_prior = @prior_noser;
mdl_base.hyperparameter.value = .2;

elems= mdl_base.fwd_model.elems;
nodes= mdl_base.fwd_model.nodes;
e= size(elems,1);


for model = 1:3
   if model==1
% Model 1: coarse==fine. each elem has a parameter
      params= 1:e; 
   elseif model==2
% Model 2: coarse model, inner circle has one parameter
      params= [1,1,1,1, 2:e-3];
   elseif model==3
% Model 3: coarse model, top left slice has one parameter
      params= 1:e;
      params([4,8,15:16,23:24,34:36])= 0;
      [jnk1,jnk2,params]= unique(params);
   end

% Create inverse_model
   imdl(model)= mdl_base;
   imdl(model).fwd_model.coarse2fine = sparse(1:e,params,1,e,max(params));

   subplot(2,3, model)
   show_fem(imdl(model).fwd_model);

% Show parameter numbers
   numeros= reshape(sprintf('%2d',params),2,e)';
   xc=mean(reshape(nodes(elems,1),e,3),2);
   yc=mean(reshape(nodes(elems,2),e,3),2);
   text(xc,yc,numeros,'FontSize',8, ...
            'HorizontalAlignment','center');

end

print_convert dual_model02a.png

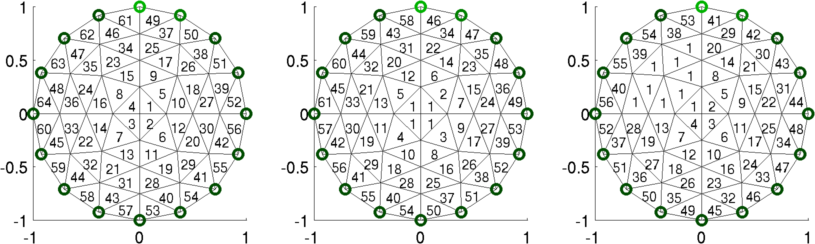
Figure: Left "Fine" mesh (64 parameters) Middle Coarse mesh (61 parameters) Right Coarse mesh (56 parameters)

Coarse to Fine Mapping

   % fine_param_1 == coarse_param_1
   % fine_param_2 == coarse_param_2
   % fine_param_3 == coarse_param_3
   % fine_param_4 == coarse_param_3

   [ 1 0 0 ] [ coarse_param_1 ]   [ fine_param_1 ]
   [ 0 1 0 ] [ coarse_param_2 ] = [ fine_param_2 ]
   [ 0 0 1 ] [ coarse_param_3 ]   [ fine_param_3 ]
   [ 0 0 1 ]                      [ fine_param_4 ]

Image Reconstructions

% Simulate data $Id: dual_model03.m 2162 2010-04-04 20:49:45Z aadler $

for model= 1:3
   img= inv_solve(imdl(model), vh, vi);
   subplot(2,3,model)
   show_fem(img);
end

print_convert dual_model03a.png;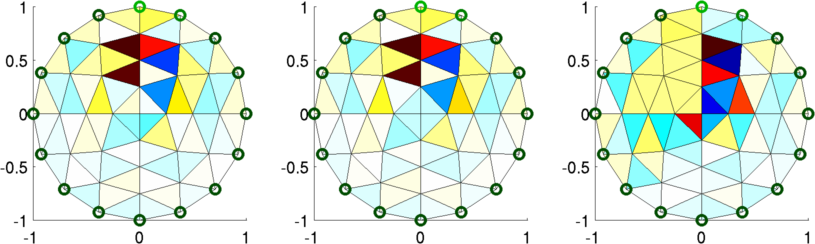

Figure: Reconstructed images. Left "Fine" mesh (64 parameters) Middle Coarse mesh (61 parameters) Right Coarse mesh (56 parameters)

Example #2: Fine and Coarse meshes

% create fine meshes $Id: dual_model04.m 4839 2015-03-30 07:44:50Z aadler $

% create base model
mdl_coarse=mk_common_model('a2c0',16);

for model = 1:3
   if model==1
% Model 1: 64 elements
      mdl_str= 'a2c0';
   elseif model==2
% Model 2: 256 elements
      mdl_str= 'b2c0';
   elseif model==3
% Model 3: 576 elements
      mdl_str= 'c2c0';
   end

   mdl_fine= mk_common_model(mdl_str,16);
   mdl_fine.fwd_model.mk_coarse_fine_mapping.n_interp= 150;
   mdl_fine.RtR_prior = @prior_noser;
   mdl_fine.hyperparameter.value = .2;

   imdl(model)= mdl_fine;
   imdl(model).fwd_model.coarse2fine = ...
       mk_coarse_fine_mapping( mdl_fine.fwd_model, mdl_coarse.fwd_model);

   subplot(2,3, model)
   show_fem(mdl_fine.fwd_model);
end

print_convert dual_model04a.png

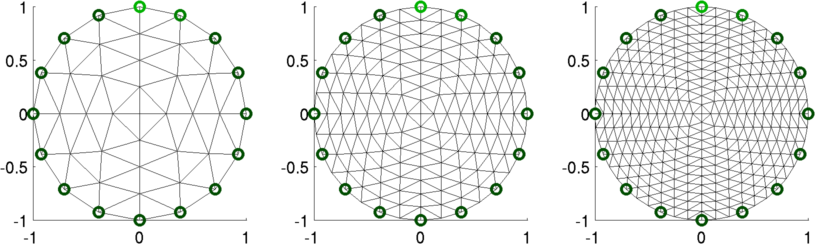
Figure: Reconstructed images. Left "Fine" mesh (64 elements) Middle Fine mesh (256 elements) Right Fine mesh (576 elements)

% Simulate data $Id: dual_model05.m 2162 2010-04-04 20:49:45Z aadler $

% Reconstruct
for model= 1:3
   img(model)= inv_solve(imdl(model), vh, vi);
end

% Show image mapped to fine model
for model= 1:3
   subplot(2,3,model)
   show_fem(img(model));
end

print_convert dual_model05b.png;

% Show image mapped to coarse model
for model= 1:3
   subplot(2,3,model)
   img(model).fwd_model = mdl_coarse.fwd_model;
   show_fem(img(model));
end

print_convert dual_model05a.png;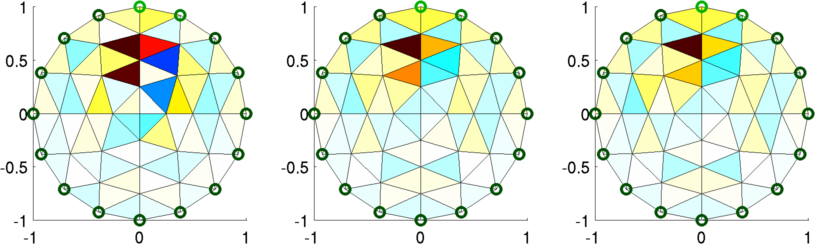

Figure: Reconstructed images mapped onto the coarse model. Left "Fine" mesh (64 elements) Middle Fine mesh (256 elements) Right Fine mesh (576 elements)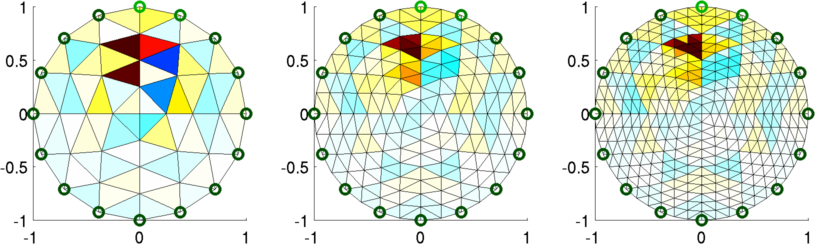

Figure: Reconstructed images mapped onto the fine model. Left "Fine" mesh (64 elements) Middle Fine mesh (256 elements) Right Fine mesh (576 elements)