SCE Carleton Logo
  Carleton > Engineering > SCE > Faculty > A. Adler > Courses > ELG7173 > Assignment 1

 

ELG 7173 - Assignment #1

  1. X-ray imaging: Beam Hardening

    2. Consider a parallel beam X ray source which outputs the following energy distribution
    Number of Photons Photon Energy
    106   10 keV  
    105   20 keV  
    104   30 keV  
    103   40 keV  
    102   50 keV  

    The X-rays travel through a mixture of soft tissue and bone. At these frequencies, these tissues have the following attenuation coefficients:

    Photon Energy Attenuation Coefficient
    of Bone     		Attenuation Coefficient
    of Soft Tissue
    10 keV   2.7 cm-1   0.6 cm-1  
    20 keV   0.43 cm-1   0.25 cm-1  
    30 keV   0.28 cm-1   0.20 cm-1  
    40 keV   0.24 cm-1   0.19 cm-1  
    50 keV   0.20 cm-1   0.18 cm-1  
    X-rays are emitted from a parallel ray source toward the target in figure 1. Measurements A and B represent the energy of photons captured after travelling through the target. The contrast is ( A − B ) / B.

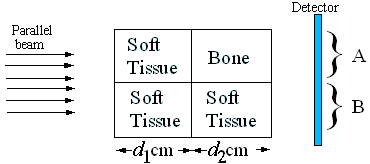
    Figure 1: X-ray source, target and detector
    • (5 Marks) Two different objects are measured. Object #1 has d1=9 cm, and d2=1 cm. Object #2 has d1=4 cm, and d2=1 cm. What is the contrast for each object?
    • (5 Marks) Briefly explain the effect of "beam hardening" in your result?

  2. X-ray imaging #2

    1. (5 Marks) Bone is more dense than soft tissue and has a significantly larger composition in heavier chemical elements (e.g. Heymsfield et al, (1991) "Chemical and elemental analysis of humans in vivo using improved body composition models", AJP - Endocrinology and Metabolism, 261(2):E190-E198 ) Describe how each of these effects results in bone having a higher X-ray attenuation than soft tissue
    2. (5 Marks) One way to increase contrast in X-ray images is to inject contrast agents, such as iodine, into the blood. For example Angiography images are done this way. Does iodine have higher or lower attenuation than soft tissue? Why?

  3. Computed Tomography

    4. The following function makeproj calculates CT projections from matrix image data. 
          function proj= makeproj( a, x, y)
        dointerpolate=1;

        if ~all(diff([size(x),size(y)])==0);
           error('x and y must be square');
        end

        rmax= max([abs(x(:));abs(y(:))]);
        spc = max(abs([mean(mean(diff(x'))), mean(mean(diff(y ))) ]));
        plen= size(x,1);

        %create x indices of projection ray
        xx=x*sin(a) + y*cos(a);
        xidx= (xx + rmax) / spc + 1;
        xi_l=  floor(xidx);     xi_h =  xi_l+1;
        xi_il= (xi_h-xidx);     xi_ih= (xidx-xi_l);

        %create y indices of projection ray
        yy=x*cos(a) - y*sin(a);
        yidx= (yy + rmax) / spc + 1;
        yi_l=  floor(yidx);     yi_h =  yi_l+1;
        yi_il= (yi_h-yidx);     yi_ih= (yidx-yi_l);

        % keep elements within bounds
        kp = (xx.^2 + yy.^2) < (rmax - spc);
        pnum = ones(plen,1) * (1:plen); pnum = pnum(kp);

        % create sparse approximation matrix
    if dointerpolate
        posn =  [ yi_l(kp), yi_h(kp), yi_l(kp), yi_h(kp)] + ...
          plen*([ xi_l(kp), xi_l(kp), xi_h(kp), xi_h(kp)]-1);
        aprx =  [xi_il(kp).*yi_il(kp), xi_il(kp).*yi_ih(kp), ...
                 xi_ih(kp).*yi_il(kp), xi_ih(kp).*yi_ih(kp)];
        proj = sparse( [pnum,pnum,pnum,pnum], posn, aprx,plen,plen^2);
    else
        xi_r= round(xidx); yi_r= round(yidx);
        posn =  yi_r(kp) + plen*(xi_r(kp)-1);
        proj = sparse( pnum, posn, 1 ,plen,plen^2);
    end
    A sample usage of this code to implement (non-filtered) simple backprojection is as follows: 
          spc=.025; rlim=1;
    [x,y]= meshgrid(-rlim:spc:rlim,-rlim:spc:rlim);
    plen= size(x,1);
    img = (x.^2 + y.^2) > rlim;
    img( x >.45 & x<.65 & y>-.05 & y<.45) =1;
    img( x >-.55 & x<-.25 & y>.45 & y<.65) =1;

    i=1; proj= zeros(plen,6);
    for ang= [0:30:150];
      prm= makeproj(ang*(pi/180),x,y);
      proj(:,i) = prm* img(:);
      i=i+1;
    end

    imbp= zeros(size(img));
    i=1;
    for ang= [0:30:150];
      prm= makeproj(ang*(pi/180),x,y);
      imbp= imbp + reshape( prm' * proj(:,i) , plen, plen);
      i=i+1;
    end
    imbp = imbp + max(imbp(:))*(  x.^2 + y.^2 > rlim );

    imagesc(imbp);
    Using this sample code, we investigate the noise properties of simple backprojection and filtered backprojection.
    1. (5 Marks) Increase the number of projection angles. Show at least two images of low and high quality images

      Comment on the improvement in image quality with number of projections. Roughly, at what number of projections, does the quality improvement become less apparent?

    2. (15 Marks) Implement the "filtered backprojection" or "convolution backprojection" algorithm (your choice), by modifying the given code to prefilter the projection data. If you wish, you may also implement any other CT reconstruction although this will be more difficult.

      Comment on the improvement in image quality with your implemented technique. Are there any noise problems with this technique?

  4. Computed Tomography #2

    5. Consider the geometry defined in the following figure for a model of a computed tomography system. Seven hexagonal regions, R1 to R7 are defined. Each region is 2 cm wide between parallel faces. Regions R1, R2, R3 R5, R6, and R7 are soft tissue, and region R4 is bone. The attenuation coefficient for bone is 1.2 cm−1, and for soft tissue is 0.5 cm−1.

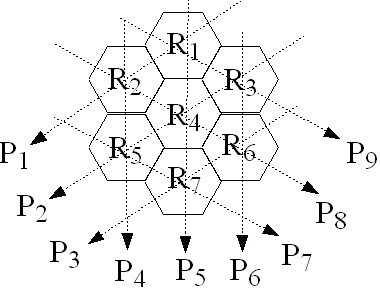
    Figure: Geometry for CT system
    1. (5 marks) Each projection has 106 input X-ray photons. Define each projection to be P=½ln( Nin/Nout) Calculate P1 ... P9
    2. (5 marks) Write the matrix equation relating the vector of region attenuations ( R1 ... R7) to the vector of projections ( P1 ... P9)
    3. (5 marks) Write a function to calculate the region attenuations using ART. How accurate is your estimate after three iterations?

Last Updated: $Date: 2007-01-22 14:44:23 -0500 (Mon, 22 Jan 2007) $