Now that you’ve got some experience with trees, and have some idea of what balance and rotations are all about, it’s time to go for the whole enchilada and deal with a tree that automatically stays balanced as it grows.

To start with, we’ll need to have all nodes contain a “balance factor”. A node’s balance factor is the height of its right subtree minus the height of its left subtree. In a balanced tree, all nodes must have a balance factor of –1 (left subtree one higher than the right subtree), 0 (left and right subtrees have the same height), or +1 (right subtree one higher than the left subtree). The reverse is also true. If all of the nodes in a tree have a balance factors are –1, 0, or 1, then the tree is balanced. In the example tree below, the balance factor for each of the nodes is shown in parentheses.

Now consider the effects of adding 45 to this tree. First we add a new node (with a balance factor of zero) in the usual way. Then work our way back to the root, making any necessary adjustments to node balance factors on the way. Node 50 has seen an increase in the height of its left subtree. Its balance factor therefore changes from +1 to 0. Node 40, on the other hand, has not seen an increase in the height of its right subtree. Therefore its balance factor of is unaffected.

Now consider the effects of adding 100 to the updated tree. As always, the new node gets a balance factor of 0. Node 70 sees an increase in the height of its right subtree, as do nodes 50 and 40. The balance factors for these nodes therefore all increase by 1.

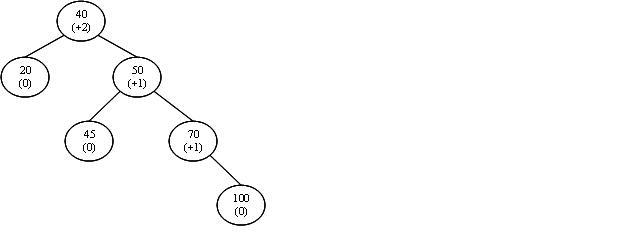
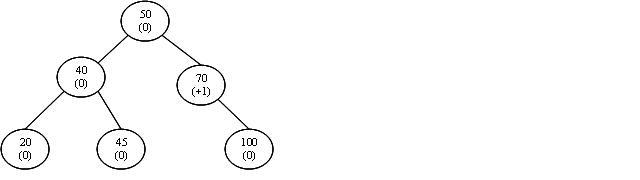
As a balance factor of +2 is unacceptable (remember – we want a balanced tree!) we must somehow deal with the situation. As the problem node (node 40) is right heavy, and its right child (node 50) is also right heavy, the appropriate action is an RR (right, right – now you know where the term came from) rotation about node 40. Performing this rotation produces the following balanced tree. Note that the balance factors of nodes 40 and 50 have become zero and that all other balance factors are unchanged.

Tree balancing involves four possible rotations – the two you explored in assignment 8 and two others. The full set of four rotations is illustrated below.

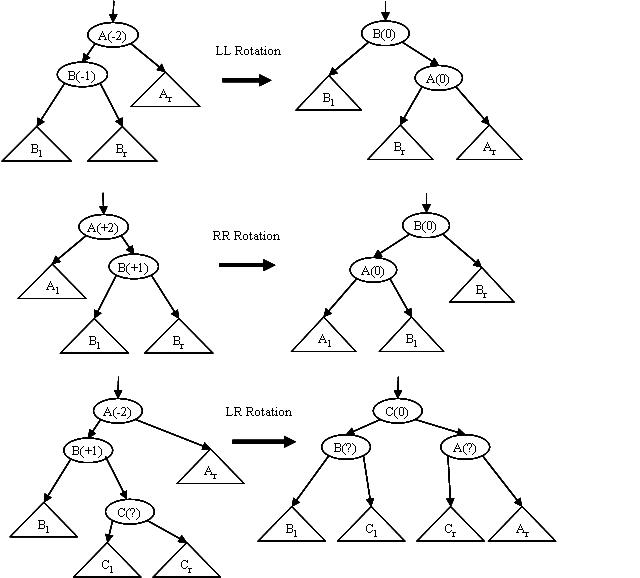
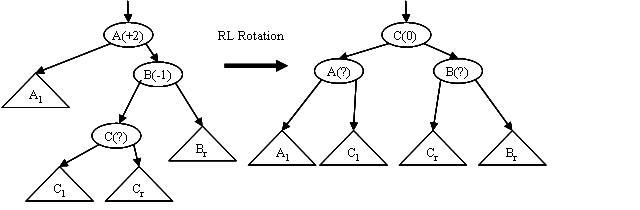
An RR rotation is performed when a node that has become too right heavy (balance factor = +2) has a right child which is also right heavy. Similarly, an LL rotation is performed when a node that has become too left heavy (balance factor = -2) has a left child which is also left heavy. A RL rotation is called for when a node which has become too right heavy has a right child which is left heavy, and an LR rotation is needed when a node which has become too left heavy has a left child which is right heavy.

In the case of RL and LR rotations, the final balance factors of nodes A and B depend upon the initial balance factor of node C, but the logic is not complex and in any case you needn’t worry about it. Methods for all four of the rotations are supplied, and these look after adjusting the balance factors. All you need be aware of is that, if a rotation is called for, the height of the resulting tree will be exactly what it was before the insertion was performed (i.e. if we do any kind of rotation, the parent of the node where the rotation is performed will not see any change in the height of its subtrees).

You have only to write one method. The prototype for this method is:

bool subInsert (TNode *&subRoot, int data, bool &heightChanged);

Given the root pointer for a subtree, the method inserts “data” into this subtree. It returns true if the insertion is successful (value does not already exist) and false otherwise. It also “returns” (via call-by-reference) whether or not the insertion affected the height of the subtree. Needless to say, the method looks after all required balance factor updates.

Consider the general case of inserting into a tree (below).

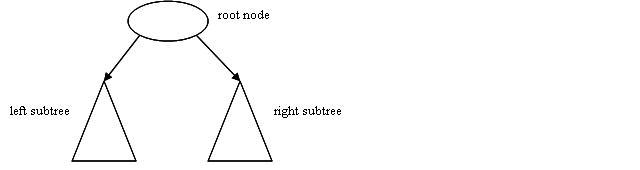
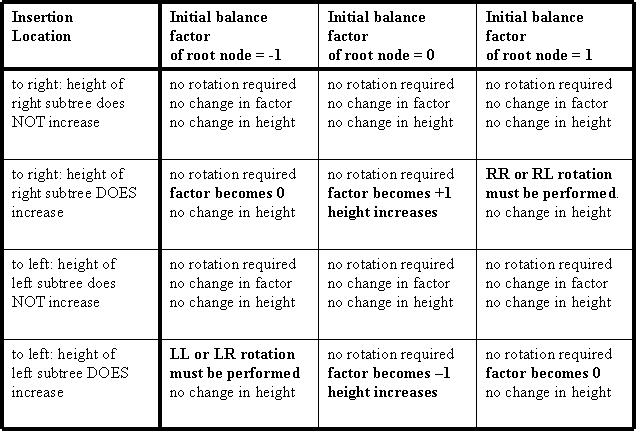
The insertion can go into either the left subtree or the right subtree. Whichever subtree it goes into, the height of this subtree may or may not increase. And finally, the root node may initially have a balance factor of –1, 0 , or +1. There are thus a grand total of 12 possible cases to be considered. The table on the next page indicates, for each of these cases, whether or not a rotation is required, what the root’s new balance factor will be, and whether or not there will be any change in the overall height of the tree.

A suitable Tree.h and a skeletal Tree.cpp (called skeleton.cpp) have been provided. You need only rename skeleton.cpp to Tree.cpp and write the required method. Note that skeleton.cpp cannot be posted until after assignment #8 is due (for obvious reasons!). In the meantime, partialskeleton.cpp contains everything except the rotation methods.

It is suggested that you begin by looking at the rotation methods supplied. These include debugging code intended to help you along. If any of the methods are used inappropriately, an error message is output and no rotation is performed. This feature requires that, before performing a rotation, the balance factor for the node involved must actually be set to –2 or +2 (as appropriate). This is actually the natural way of doing things: first update the balance factor, and then see if a rotation is required.

Submit just one file: Tree.cpp.

Updated: Tuesday, March 10th, 2009.